
Next: Runge-Kutta methods Up: 14.3.2 System Simulator Previous: Closed-form solutions
For most systems, the integration must be performed numerically. A
system simulator based on numerical integration can be constructed by
breaking ![]() into smaller intervals and iterating classical methods
for computing numerical solutions to differential equations. The
Euler method is the simplest of these methods. Let
into smaller intervals and iterating classical methods
for computing numerical solutions to differential equations. The
Euler method is the simplest of these methods. Let ![]() denote
a small time interval over which the approximation will be made. This
can be considered as an internal parameter of the system simulator.
In practice, this
denote
a small time interval over which the approximation will be made. This
can be considered as an internal parameter of the system simulator.
In practice, this ![]() is usually much smaller than the
is usually much smaller than the ![]() used in the discrete-time model of Section 14.2.2.
Suppose that
used in the discrete-time model of Section 14.2.2.
Suppose that ![]() and
and ![]() are given and the task is to estimate
are given and the task is to estimate
![]() .
.
By performing integration over time, the state transition equation can
be used to determine the state after some fixed amount of time
![]() has passed. For example, if
has passed. For example, if ![]() is given and
is given and
![]() is known over the interval
is known over the interval
![]() ,
then the state at time
,
then the state at time ![]() can be determined as
can be determined as
Using the fact that
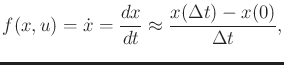 |
(14.15) |
Steven M LaValle 2020-08-14