The extension of sequential game theory to the continuous-time case is
called differential game theory (or
dynamic game theory [59]), a subject introduced by
Isaacs [477]. All of the variants considered in Sections
9.3, 9.4, 10.5 are possible:
- There may be any number of players.
- The game may be zero-sum or
nonzero-sum.
- The state may or may not be known. If the state is unknown,
then interesting I-spaces arise, similar to those of Section
11.7.
- Nature can interfere with the game.
- Different equilibrium concepts, such as saddle points and Nash
equilibria, can be defined.
See [59] for a thorough overview of differential games.
Two players,
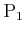 and
and
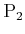 , can be engaged in a differential
game in which each has a continuous set of actions. Let
, can be engaged in a differential
game in which each has a continuous set of actions. Let 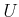 and
and 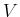 denote the action spaces of
denote the action spaces of
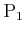 and
and
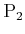 , respectively. A state
transition equation can be defined as
, respectively. A state
transition equation can be defined as
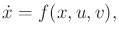 |
(13.203) |
in which 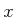 is the state,
is the state, 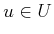 , and
, and 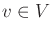 .
.
Linear differential games are an
important family of games because many techniques from optimal control
theory can be extended to solve them [59].
Example 13..17 (Linear Differential Games)
The linear system model (
13.37) can be extended to
incorporate two players. Let
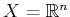
be a phase space. Let
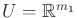
and
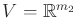
be an action spaces for
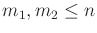
. A
linear differential game is expressed as
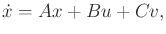 |
(13.204) |
in which
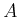
,
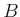
, and
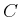
are constant, real-valued matrices of
dimensions
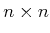
,
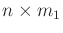
, and
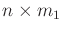
,
respectively. The particular solution to such games depends on the
cost functional and desired equilibrium concept. For the case of
a quadratic cost, closed-form solutions exist. These extend techniques
that are developed for linear systems with one decision maker; see
Section
15.2.2 and [
59].
The original work of Isaacs [477] contains many interesting
examples of pursuit-evasion
differential games. One of the most
famous is described next.
Example 13..18 (Homicidal Chauffeur)
In the
homicidal chauffeur game,
the pursuer is a Dubins car
and the evader is a point robot that
can translate in any direction. Both exist in the same world,
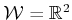
. The speeds of the car and robot are
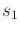
and
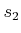
,
respectively. It is assumed that
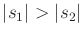
, which means that
the pursuer moves faster than the evader. The transition equation is
given by extending (
13.15) to include two state
variables that account for the robot position:
The state space is

is
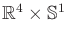
, and the action spaces
are
![$ U = [-\phi_{max},\phi_{max}]$](img6114.gif)
and
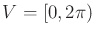
.
The task is to determine whether the pursuer can come within some
prescribed distance 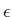 of the evader:
of the evader:
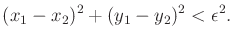 |
(13.206) |
If this occurs, then the pursuer wins; otherwise, the evader wins.
The solution depends on the
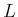
,
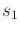
,
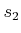
,
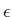
, and the
initial state. Even though the pursuer moves faster, the evader may
escape because it does not have a limited turning radius. For given
values of
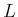
,
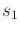
,
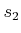
, and
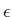
, the state space

can
be partitioned into two regions that correspond to whether the pursuer
or evader wins [
59,
477]. To gain some intuition about
how this partition may appear, imagine the motions that a bullfighter
must make to avoid a fast, charging bull (yes, bulls behave very much
like a fast Dubins car when provoked).

Another interesting pursuit-evasion game arises in the case of one car
attempting to intercept another [694].
Example 13..19 (A Game of Two Cars)
Imagine that there are two simple cars that move in the same world,
. Each has a transition equation given by
(
13.15). The state transition equation for the game is
The pursuit-evasion game becomes very interesting if both players are
restricted to be Dubins cars.

Steven M LaValle
2020-08-14

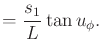
![]() of the evader:
of the evader: