
Next: Further Reading Up: 12.5.2 Nonprehensile Manipulation Previous: 12.5.2 Nonprehensile Manipulation
Another example of sensorless manipulation will now be described,
which was developed by Goldberg and Mason in
[394,395,396]; see also [681]. A Java
implementation of the algorithm appears in [131]. Suppose
that convex, polygonal parts arrive individually along a conveyor belt
in a factory. They are to be used in an assembly operation and need
to be placed into a given orientation. Figure 12.50 shows
a top view of a parallel-jaw gripper. The robot can perform a
squeeze operation by bringing the jaws together. Figure
12.50a shows the part before squeezing, and Figure
12.50b shows it afterward. A simple model is assumed for
the mechanics. The jaws move at constant velocity toward each other,
and it is assumed that they move slowly enough so that dynamics can be
neglected. To help slide the part into place, one of the jaws may be
considered as a frictionless contact (this is a real device; see
[175]). The robot can perform a squeeze operation at any
orientation in ![]() (actually, only
(actually, only ![]() is needed due to
symmetry). Let
is needed due to
symmetry). Let
![]() denote the set of all squeezing
actions. Each squeezing action terminates on its own after the part
can be squeezed no further (without crushing the part).
denote the set of all squeezing
actions. Each squeezing action terminates on its own after the part
can be squeezed no further (without crushing the part).
The planning problem can be modeled as a game against nature. The
initial orientation,
![]() , of the part is chosen by
nature and is unknown. The state space is
, of the part is chosen by
nature and is unknown. The state space is
![]() . For a given part,
the task is to design a sequence,
. For a given part,
the task is to design a sequence,
| (12.35) |
| (12.36) |
Consider how a part in an unknown orientation behaves. Due to
rotational symmetry, it will be convenient to describe the effect of a
squeeze operation based on the relative angle between the part and the
robot. Therefore, let
![]() , assuming arithmetic modulo
, assuming arithmetic modulo ![]() . Initially,
. Initially, ![]() may assume any value in
may assume any value in ![]() . It
turns out that after one squeeze,
. It
turns out that after one squeeze, ![]() is always forced into one
of a finite number of values. This can be explained by representing
the diameter function
is always forced into one
of a finite number of values. This can be explained by representing
the diameter function ![]() , which indicates the maximum
thickness that can be obtained by taking a slice of the part at
orientation
, which indicates the maximum
thickness that can be obtained by taking a slice of the part at
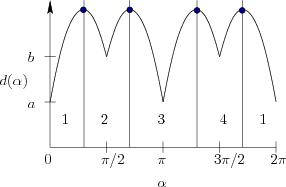
orientation ![]() . Figure 12.51 shows the slice for
a rectangle. The local minima of the distance function indicate
orientations at which the part will stabilize as shown in Figure
12.50b. As the part changes its orientation during the
squeeze operation, the
. Figure 12.51 shows the slice for
a rectangle. The local minima of the distance function indicate
orientations at which the part will stabilize as shown in Figure
12.50b. As the part changes its orientation during the
squeeze operation, the ![]() value changes in a way that gradually
decreases
value changes in a way that gradually
decreases ![]() . Thus,
. Thus, ![]() can be divided into regions
of attraction, as shown in Figure 12.52. These behave
much like the funnels in Section
8.5.1.
can be divided into regions
of attraction, as shown in Figure 12.52. These behave
much like the funnels in Section
8.5.1.
 |
The critical observation to solve the problem without sensors is that
with each squeeze the uncertainty can grow no worse, and is usually
reduced. Assume ![]() is fixed. For the state transition equation
is fixed. For the state transition equation
![]() , the same
, the same ![]() will be produced for an interval of values
for
will be produced for an interval of values
for ![]() . Due to rotational symmetry, it is best to express this in
terms of
. Due to rotational symmetry, it is best to express this in
terms of ![]() . Let
. Let ![]() denote relative orientation
obtained after a squeeze. Since
denote relative orientation
obtained after a squeeze. Since ![]() is a function of
is a function of ![]() and
and
![]() , this can be expressed as a squeeze function,
, this can be expressed as a squeeze function,
![]() , defined as
, defined as
| (12.37) |
 |
(12.38) |
Any interval
![]() can be interpreted as a
nondeterministic I-state, based on the history of squeezes that have
been performed. It is defined, however, with respect to relative
orientations, instead of the original states. The algorithms
discussed in Section 12.1.2 can be applied to
can be interpreted as a
nondeterministic I-state, based on the history of squeezes that have
been performed. It is defined, however, with respect to relative
orientations, instead of the original states. The algorithms
discussed in Section 12.1.2 can be applied to
![]() . A backward search algorithm is given in
[395] that starts with a singleton, nondeterministic I-state.
The planning proceeds by performing a backward search on
. A backward search algorithm is given in
[395] that starts with a singleton, nondeterministic I-state.
The planning proceeds by performing a backward search on
![]() .
In each iteration, the interval,
.
In each iteration, the interval, ![]() , of possible relative
orientations increases until eventually all of
, of possible relative
orientations increases until eventually all of
![]() is reached (or
the period of symmetry, if symmetries exist).
is reached (or
the period of symmetry, if symmetries exist).
The algorithm is greedy in the sense that it attempts to force ![]() to
be as large as possible in every step. Note from Figure
12.52 that the regions of attraction are maximal at
the minima of the diameter function. Therefore, only the minima
values are worth considering as choices for
to
be as large as possible in every step. Note from Figure
12.52 that the regions of attraction are maximal at
the minima of the diameter function. Therefore, only the minima
values are worth considering as choices for ![]() . Let
. Let ![]() denote
the preimage of the function
denote
the preimage of the function ![]() . In the first step, the algorithm
finds the
. In the first step, the algorithm
finds the ![]() for which
for which ![]() is largest (in terms of
length in
is largest (in terms of
length in
![]() ). Let
). Let ![]() denote this relative orientation,
and let
denote this relative orientation,
and let
![]() . For each subsequent iteration, let
. For each subsequent iteration, let ![]() denote the largest interval in
denote the largest interval in ![]() that satisfies
that satisfies
Suppose that the sequence
![]() has been computed.
This must be transformed into a plan that is expressed in terms of a
fixed coordinate frame for the robot. The
has been computed.
This must be transformed into a plan that is expressed in terms of a
fixed coordinate frame for the robot. The ![]() -step action sequence
-step action sequence
![]() is recovered from
is recovered from
Steven M LaValle 2020-08-14