The continuous-space methods from Section 10.6 can be
directly applied to produce an approximate solution by interpolating
over 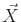 to determine cost-to-go values. The initial cost-to-go
value
to determine cost-to-go values. The initial cost-to-go
value 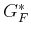 over the collection of samples is obtained by
(12.6). Following (10.46), the dynamic
programming recurrence is
over the collection of samples is obtained by
(12.6). Following (10.46), the dynamic
programming recurrence is
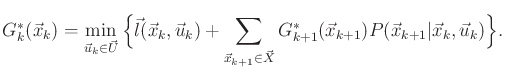 |
(12.10) |
If
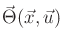 is finite, the probability mass is
distributed over a finite set of points,
is finite, the probability mass is
distributed over a finite set of points,
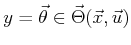 . This in turn implies that
. This in turn implies that
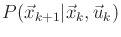 is also distributed over a finite
subset of
is also distributed over a finite
subset of 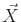 . This is somewhat unusual because
. This is somewhat unusual because 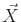 is a
continuous space, which ordinarily requires the specification of a
probability density function. Since the set of future states is
finite, this enables a sum to be used in (12.10) as opposed
to an integral over a probability density function. This technically
yields a probability density over
is a
continuous space, which ordinarily requires the specification of a
probability density function. Since the set of future states is
finite, this enables a sum to be used in (12.10) as opposed
to an integral over a probability density function. This technically
yields a probability density over 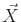 , but this density must
be expressed using Dirac functions.12.1 An approximation is still needed, however, because the
, but this density must
be expressed using Dirac functions.12.1 An approximation is still needed, however, because the
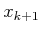 points may not be exactly the sample points on which the
cost-to-go function
points may not be exactly the sample points on which the
cost-to-go function 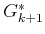 is represented.
is represented.
Steven M LaValle
2020-08-14

![]() to determine cost-to-go values. The initial cost-to-go
value
to determine cost-to-go values. The initial cost-to-go
value ![]() over the collection of samples is obtained by
(12.6). Following (10.46), the dynamic
programming recurrence is
over the collection of samples is obtained by
(12.6). Following (10.46), the dynamic
programming recurrence is