Constructing a derived information transition equation

As presented so far, the full history I-state is needed to determine a derived I-state. It may be preferable, however, to discard histories and work entirely in the derived I-space. Without storing the histories on the machine or robot, a derived information transition equation needs to be developed. The important requirement in this case is as follows:

If ${\eta}_k$ is replaced by ${\kappa}({\eta}_k)$, then ${\kappa}({\eta}_{k+1})$ must be correctly determined using only ${\kappa}({\eta}_k)$, $u_k$, and $y_{k+1}$.

Whether this requirement can be met depends on the particular I-map. Another way to express the requirement is that if ${\kappa}({\eta}_k)$ is given, then the full history ${\eta}$ does not contain any information that could further constrain ${\kappa}({\eta}_{k+1})$. The information provided by ${\kappa }$ is sufficient for determining the next derived I-states. This is similar to the concept of a sufficient statistic, which arises in decision theory [89]. If the requirement is met, then ${\kappa }$ is called a sufficient I-map. One peculiarity is that the sufficiency is relative to ${\cal I}_{der}$, as opposed to being absolute in some sense. For example, any I-map that maps onto ${\cal I}_{der}= \{0\}$ is sufficient because ${\kappa}({\eta}_{k+1})$ is always known (it remains fixed at 0). Thus, the requirement for sufficiency depends strongly on the particular derived I-space.

For a sufficient I-map, a derived information transition equation is determined as

$${\kappa}({\eta}_{k+1}) = {f_{\cal I}}_{der}({\kappa}({\eta}_k),u_k,y_{k+1}) .$$ (11.27)

The implication is that ${\cal I}_{der}$ is the new I-space in which the problem ``lives.'' There is no reason for the decision maker to consider histories. This idea is crucial to the success of many planning algorithms. Sections 11.2.2 and 11.2.3 introduce nondeterministic I-spaces and probabilistic I-spaces, which are two of the most important derived I-spaces and are obtained from sufficient I-maps. The I-map ${{\kappa}_{stage}}$ from Example 11.12 is also sufficient. The estimation I-map from Example 11.11 is usually not sufficient because some history is needed to provide a better estimate.

Figure 11.4: (a) For an I-map to be sufficient, the same result must be reached in the lower right, regardless of the path taken from the upper left. (b) The problem is that ${\kappa }$ images may contain many histories, which eventually map to multiple derived I-states.

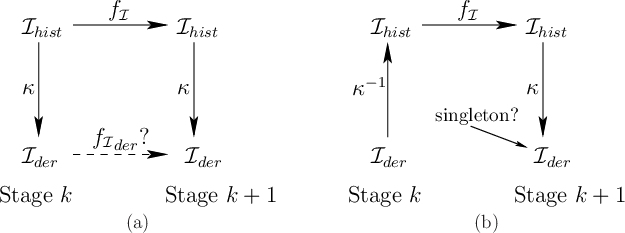The diagram in Figure 11.4a indicates the problem of obtaining a sufficient I-map. The top of the diagram shows the history I-state transitions before the I-map was introduced. The bottom of the diagram shows the attempted derived information transition equation, ${f_{\cal I}}_{der}$. The requirement is that the derived I-state obtained in the lower right must be the same regardless of which path is followed from the upper left. Either ${f_{\cal I}}$ can be applied to ${\eta}$, followed by ${\kappa }$, or ${\kappa }$ can be applied to ${\eta}$, followed by some ${f_{\cal I}}_{der}$. The problem with the existence of ${f_{\cal I}}_{der}$ is that ${\kappa }$ is usually not invertible. The preimage ${\kappa}^{-1} ({\eta}_{der})$ of some derived I-state ${\eta}_{der} \in {\cal I}_{der}$ yields a set of histories in ${\cal I}_{hist}$. Applying ${f_{\cal I}}$ to all of these yields a set of possible next-stage history I-states. Applying ${\kappa }$ to these may yield a set of derived I-states because of the ambiguity introduced by ${\kappa}^{-1}$. This chain of mappings is shown in Figure 11.4b. If a singleton is obtained under all circumstances, then this yields the required values of ${f_{\cal I}}_{der}$. Otherwise, new uncertainty arises about the current derived I-state. This could be handled by defining an information space over the information space, but this nastiness will be avoided here.

Since I-maps can be defined from any derived I-space to another, the concepts presented in this section do not necessarily require ${\cal I}_{hist}$ as the starting point. For example, an I-map, ${\kappa}: {\cal I}_{der}\rightarrow {\cal I}'_{der}$, may be called sufficient with respect to ${\cal I}_{der}$ rather than with respect to ${\cal I}_{hist}$.