2.3.1.1 Backward value iteration
As for the search methods, there are both forward and backward
versions of the approach. The backward case will be covered first.
Even though it may appear superficially to be easier to progress from
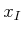 , it turns out that progressing backward from
, it turns out that progressing backward from 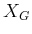 is
notationally simpler. The forward case will then be covered once some
additional notation is introduced.
is
notationally simpler. The forward case will then be covered once some
additional notation is introduced.
The key to deriving long optimal plans from shorter ones lies in the
construction of optimal cost-to-go functions over  . For
. For  from
from
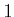 to
to 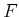 , let
, let 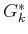 denote the cost that accumulates from stage
denote the cost that accumulates from stage
 to
to  under the execution of the optimal plan:
under the execution of the optimal plan:
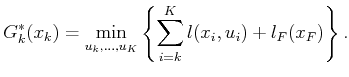 |
(2.5) |
Inside of the  of (2.5) are the last
of (2.5) are the last 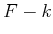 terms of
the cost functional, (2.4). The optimal cost-to-go for
the boundary condition of
terms of
the cost functional, (2.4). The optimal cost-to-go for
the boundary condition of 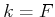 reduces to
reduces to
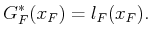 |
(2.6) |
This makes intuitive sense: Since there are no stages in which an
action can be applied, the final stage cost is immediately received.
Now consider an algorithm that makes 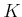 passes over
passes over  , each time
computing
, each time
computing 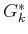 from
from 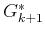 , as
, as  ranges from
ranges from  down to
down to
 . In the first iteration,
. In the first iteration, 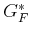 is copied from
is copied from 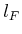 without
significant effort. In the second iteration,
without
significant effort. In the second iteration, 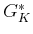 is computed
for each
is computed
for each 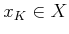 as
as
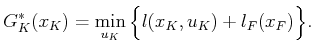 |
(2.7) |
Since
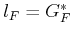 and
and
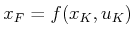 , substitutions can be
made into (2.7) to obtain
, substitutions can be
made into (2.7) to obtain
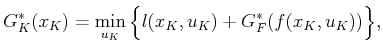 |
(2.8) |
which is straightforward to compute for each 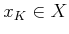 . This
computes the costs of all optimal one-step plans from stage
. This
computes the costs of all optimal one-step plans from stage 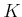 to
stage
to
stage 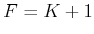 .
.
It will be shown next that 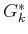 can be computed similarly once
can be computed similarly once
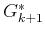 is given. Carefully study (2.5) and note that
it can be written as
is given. Carefully study (2.5) and note that
it can be written as
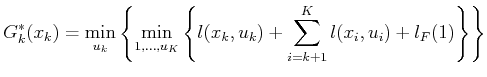 |
(2.9) |
by pulling the first term out of the sum and by separating the
minimization over 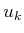 from the rest, which range from
from the rest, which range from 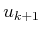 to
to
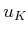 . The second
. The second 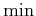 does not affect the
does not affect the
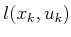 term; thus,
term; thus,
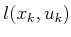 can be pulled outside to obtain
can be pulled outside to obtain
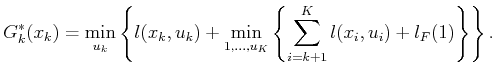 |
(2.10) |
The inner 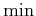 is exactly the definition of the optimal cost-to-go
function
is exactly the definition of the optimal cost-to-go
function 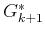 . Upon substitution, this yields the recurrence
. Upon substitution, this yields the recurrence
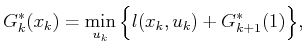 |
(2.11) |
in which
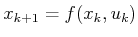 . Now that the right side of
(2.11) depends only on
. Now that the right side of
(2.11) depends only on 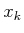 ,
, 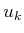 , and
, and 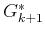 , the
computation of
, the
computation of 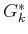 easily proceeds in
easily proceeds in
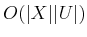 time. This computation is
called a value iteration. Note that in each value iteration,
some states receive an infinite value only because they are not
reachable; a
time. This computation is
called a value iteration. Note that in each value iteration,
some states receive an infinite value only because they are not
reachable; a 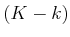 -step plan from
-step plan from 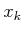 to
to 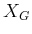 does not exist.
This means that there are no actions,
does not exist.
This means that there are no actions,
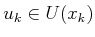 , that bring
, that bring
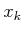 to a state
to a state
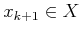 from which a
from which a 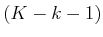 -step plan exists
that terminates in
-step plan exists
that terminates in 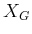 .
.
Summarizing, the value iterations proceed as follows:
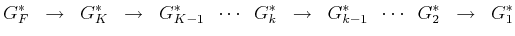 |
(2.12) |
until finally 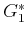 is determined after
is determined after
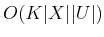 time. The
resulting
time. The
resulting 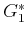 may be applied to yield
may be applied to yield
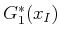 , the
optimal cost to go to the goal from
, the
optimal cost to go to the goal from 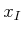 . It also conveniently
gives the optimal cost-to-go from any other initial state. This cost
is infinity for states from which
. It also conveniently
gives the optimal cost-to-go from any other initial state. This cost
is infinity for states from which 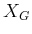 cannot be reached in
cannot be reached in 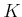 stages.
stages.
It seems convenient that the cost of the optimal plan can be computed
so easily, but how is the actual plan extracted? One possibility is
to store the action that satisfied the 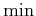 in (2.11)
from every state, and at every stage. Unfortunately, this requires
in (2.11)
from every state, and at every stage. Unfortunately, this requires
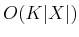 storage, but it can be reduced to
storage, but it can be reduced to 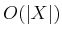 using the tricks
to come in Section 2.3.2 for the more general case of
variable-length plans.
using the tricks
to come in Section 2.3.2 for the more general case of
variable-length plans.
Example 2..3 (A Five-State Optimal Planning Problem)
Figure
2.8 shows a graph representation of a planning
problem in which
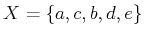
. Suppose that
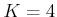
,
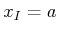
,
and
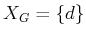
. There will hence be four value iterations, which
construct
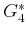
,
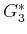
,
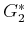
, and
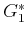
, once the
final-stage cost-to-go,
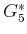
, is given.
Figure 2.8:
A five-state example. Each vertex
represents a state, and each edge represents an input that can be
applied to the state transition equation to change the state. The
weights on the edges represent
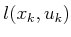 (
(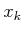 is the originating
vertex of the edge).
is the originating
vertex of the edge).
 |
Figure 2.9:
The optimal cost-to-go functions
computed by backward value iteration.
 |
Figure 2.10:
The possibilities for advancing
forward one stage. This is obtained by making two copies of the
states from Figure 2.8, one copy for the current
state and one for the potential next state.
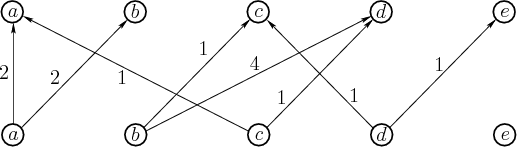 |
Figure 2.11:
By turning Figure 2.10
sideways and copying it 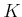 times, a graph can be drawn that easily
shows all of the ways to arrive at a final state from an initial state
by flowing from left to right. The computations automatically select
the optimal route.
times, a graph can be drawn that easily
shows all of the ways to arrive at a final state from an initial state
by flowing from left to right. The computations automatically select
the optimal route.
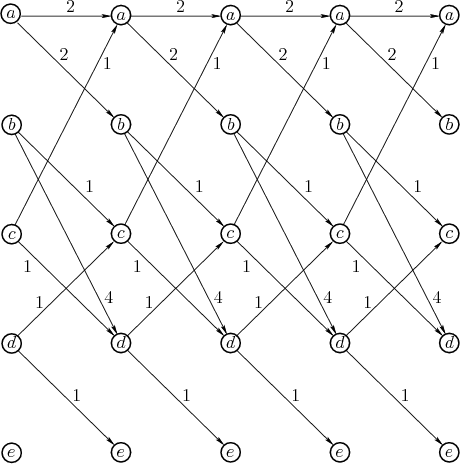 |
The cost-to-go functions are shown in Figure 2.9.
Figures 2.10 and 2.11 illustrate the
computations. For computing 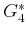 , only
, only 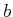 and
and 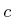 receive
finite values because only they can reach
receive
finite values because only they can reach 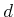 in one stage. For
computing
in one stage. For
computing 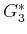 , only the values
, only the values
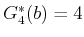 and
and
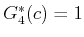 are important. Only paths that reach
are important. Only paths that reach 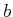 or
or 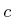 can possibly
lead to
can possibly
lead to 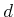 in stage
in stage 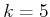 . Note that the minimization in
. Note that the minimization in
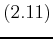 always chooses the action that produces the lowest
total cost when arriving at a vertex in the next stage.
always chooses the action that produces the lowest
total cost when arriving at a vertex in the next stage.

Steven M LaValle
2020-08-14

![]() , it turns out that progressing backward from
, it turns out that progressing backward from ![]() is
notationally simpler. The forward case will then be covered once some
additional notation is introduced.
is
notationally simpler. The forward case will then be covered once some
additional notation is introduced.
![]() . For
. For ![]() from
from
![]() to
to ![]() , let
, let ![]() denote the cost that accumulates from stage
denote the cost that accumulates from stage
![]() to
to ![]() under the execution of the optimal plan:
under the execution of the optimal plan:
![]() passes over
passes over ![]() , each time
computing
, each time
computing ![]() from
from ![]() , as
, as ![]() ranges from
ranges from ![]() down to
down to
![]() . In the first iteration,
. In the first iteration, ![]() is copied from
is copied from ![]() without
significant effort. In the second iteration,
without
significant effort. In the second iteration, ![]() is computed
for each
is computed
for each ![]() as
as
![]() can be computed similarly once
can be computed similarly once
![]() is given. Carefully study (2.5) and note that
it can be written as
is given. Carefully study (2.5) and note that
it can be written as
![]() in (2.11)
from every state, and at every stage. Unfortunately, this requires
in (2.11)
from every state, and at every stage. Unfortunately, this requires
![]() storage, but it can be reduced to
storage, but it can be reduced to ![]() using the tricks
to come in Section 2.3.2 for the more general case of
variable-length plans.
using the tricks
to come in Section 2.3.2 for the more general case of
variable-length plans.



![]() , only
, only ![]() and
and ![]() receive
finite values because only they can reach
receive
finite values because only they can reach ![]() in one stage. For
computing
in one stage. For
computing ![]() , only the values
, only the values
![]() and
and
![]() are important. Only paths that reach
are important. Only paths that reach ![]() or
or ![]() can possibly
lead to
can possibly
lead to ![]() in stage
in stage ![]() . Note that the minimization in
. Note that the minimization in
![]() always chooses the action that produces the lowest
total cost when arriving at a vertex in the next stage.
always chooses the action that produces the lowest
total cost when arriving at a vertex in the next stage.
![]()