2.2.4 A Unified View of the Search Methods
It is convenient to summarize the behavior of all search methods in
terms of several basic steps. Variations of these steps will appear
later for more complicated planning problems. For example, in Section
5.4, a large family of sampling-based motion planning
algorithms can be viewed as an extension of the steps presented here.
The extension in this case is made from a discrete state space to a
continuous state space (called the configuration space). Each method
incrementally constructs a search graph,
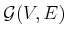 , which is the
subgraph of the state transition graph that has been explored so far.
, which is the
subgraph of the state transition graph that has been explored so far.
All of the planning methods from this section followed the same basic
template:
- Initialization: Let the search graph,
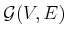 , be
initialized with
, be
initialized with 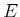 empty and
empty and 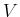 containing some starting states.
For forward search,
containing some starting states.
For forward search,
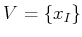 ; for backward search,
; for backward search,
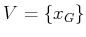 . If bidirectional search is used, then
. If bidirectional search is used, then
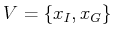 . It is possible to grow more than two trees and
merge them during the search process. In this case, more states can
be initialized in
. It is possible to grow more than two trees and
merge them during the search process. In this case, more states can
be initialized in  . The search graph will incrementally grow to
reveal more and more of the state transition graph.
. The search graph will incrementally grow to
reveal more and more of the state transition graph.
- Select Vertex: Choose a vertex
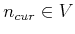 for
expansion; this is usually accomplished by maintaining a priority
queue. Let
for
expansion; this is usually accomplished by maintaining a priority
queue. Let 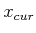 denote the state associated with
denote the state associated with 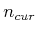 .
.
- Apply an Action: In either a forward or backward
direction, a new state,
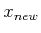 , is obtained. This may arise from
, is obtained. This may arise from
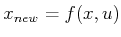 for some
for some
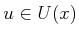 (forward) or
(forward) or
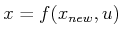 for some
for some
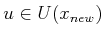 (backward).
(backward).
- Insert a Directed Edge into the Graph: If certain
algorithm-specific tests are passed, then generate an edge from
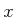 to
to
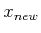 for the forward case, or an edge from
for the forward case, or an edge from 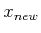 to
to 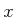 for
the backward case. If
for
the backward case. If 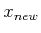 is not yet in
is not yet in 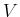 , it will be
inserted into
, it will be
inserted into 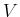 .2.2
.2.2
- Check for Solution: Determine whether
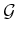 encodes a
path from
encodes a
path from 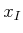 to
to 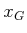 . If there is a single search tree,
then this is trivial. If there are two or more search trees, then
this step could be expensive.
. If there is a single search tree,
then this is trivial. If there are two or more search trees, then
this step could be expensive.
- Return to Step 2: Iterate unless a solution has been found
or an early termination condition is satisfied, in which case the
algorithm reports failure.
Note that in this summary, several iterations may have to be made to
generate one iteration in the previous formulations. The forward
search algorithm in Figure 2.4 tries all actions for the
first element of 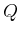 . If there are
. If there are 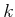 actions, this corresponds
to
actions, this corresponds
to 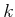 iterations in the template above.
iterations in the template above.
Steven M LaValle
2020-08-14

![]() . If there are
. If there are ![]() actions, this corresponds
to
actions, this corresponds
to ![]() iterations in the template above.
iterations in the template above.