
Next: Average cost-per-stage Up: 10.3.1 Problem Formulation Previous: 10.3.1 Problem Formulation
In Formulation 10.2, the cost functional in Item
6 must be defined carefully to ensure that finite
values are always obtained, even though the number of stages tends to
infinity. The discounted cost model provides one simple way to
achieve this by rapidly decreasing costs in future stages. Its
definition is based on the standard geometric series. For any
real parameter
![]() ,
,
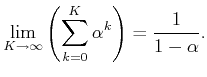 |
(10.65) |
Now let
![]() denote a discount factor, which is
applied in the definition of a cost functional:
denote a discount factor, which is
applied in the definition of a cost functional:
The rate of cost decrease depends strongly on ![]() . For example,
if
. For example,
if
![]() , the costs decrease very rapidly. If
, the costs decrease very rapidly. If
![]() , the convergence to zero is much slower. The trade-off is that
with a large value of
, the convergence to zero is much slower. The trade-off is that
with a large value of ![]() , more stages are taken into account,
and the designed plan is usually of higher quality. If a small value
of
, more stages are taken into account,
and the designed plan is usually of higher quality. If a small value
of ![]() is used, methods such as value iteration converge much
more quickly; however, the solution quality may be poor because of
``short sightedness.''
is used, methods such as value iteration converge much
more quickly; however, the solution quality may be poor because of
``short sightedness.''
The term
![]() in (10.67) assumes
different values depending on
in (10.67) assumes
different values depending on ![]() ,
, ![]() , and
, and ![]() . Since
there are only a finite number of possibilities, they must be bounded
by some positive constant
. Since
there are only a finite number of possibilities, they must be bounded
by some positive constant ![]() .10.1 Hence,
.10.1 Hence,
Steven M LaValle 2020-08-14