9.3.3.2 Computation of randomized saddle points

So far it has been established that a randomized saddle point always exists, but how can one be found? Two key observations enable a combinatorial solution to the problem:

1. The security strategy for each player can be found by considering only deterministic strategies for the opposing player.
2. If the strategy for the other player is fixed, then the expected cost is a linear function of the undetermined probabilities.

First consider the problem of determining the security strategy for ${{\rm P}_1}$. The first observation means that (9.59) does not need to consider randomized strategies for ${{\rm P}_2}$. Inside of the $\operatornamewithlimits{argmin}$, $w$ is fixed. What randomized strategy, $z \in Z$, maximizes ${\bar{L}}(w,z) = wAz$? If $w$ is fixed, then $wA$ can be treated as a constant $n$-dimensional vector, $s$. This means ${\bar{L}}(w,z) = s \cdot z$, in which $\cdot$ is the inner (dot) product. Now the task is to select $z$ to maximize $s \cdot z$. This involves selecting the largest element of $s$; suppose this is $s_i$. The maximum cost over all $z \in Z$ is obtained by placing all of the probability mass at action $i$. Thus, the strategy $z_i = 1$ and $z_j = 0$ for $i \neq j$ gives the highest cost, and it is deterministic.

Using the first observation, for each $w \in W$, only $n$ possible responses by ${{\rm P}_2}$ need to be considered. These are the $n$ deterministic strategies, each of which assigns $z_i = 1$ for a unique $i \in \{1,\ldots,n\}$.

Now consider the second observation. The expected cost, ${\bar{L}}(w,z) = wAz$, is a linear function of $w$, if $z$ is fixed. Since $z$ only needs to be fixed at $n$ different values due to the first observation, $w$ is selected at the point at which the smallest maximum value among the $n$ linear functions occurs. This is the minimum value of the upper envelope of the collection of linear functions. Such envelopes were mentioned in Section 6.5.2. Example 9.16 will illustrate this. The domain for this optimization can conveniently be set as a triangle in ${\mathbb{R}}^{m-1}$. Even though $W \subset {\mathbb{R}}^m$, the last coordinate, $w_m$, is not needed because it is always $w_m = 1 - (w_1 + \cdots + w_{m-1})$. The resulting optimization falls under linear programming, for which many combinatorial algorithms exist [259,264,664,731].

In the explanation above, there is nothing particular to ${{\rm P}_1}$ when trying to find its security strategy. The same method can be applied to determine the security strategy for ${{\rm P}_2}$; however, every minimization is replaced by a maximization, and vice versa. In summary, the $\min$ in (9.60) needs only to consider the deterministic strategies in $W$. If $w$ becomes fixed, then ${\bar{L}}(w,z) = wAz$ is once again a linear function, but this time it is linear in $z$. The best randomized action is chosen by finding the point $z \in Z$ that gives the highest minimum value among $m$ linear functions. This is the minimum value of the lower envelope of the collection of linear functions. The optimization occurs over ${\mathbb{R}}^{n-1}$ because the last coordinate, $z_n$, is obtained directly from $z_n = 1 - (z_1 + \cdots + z_{n-1})$.

This computation method is best understood through an example.

Example 9..16 (Computing a Randomized Saddle Point)   The simplest case is when both players have only two actions. Let the cost matrix be defined as

$$\begin{tabular}{cc} & $V$\ \\ $U$\ & \begin{tabular}{\vert c\vert c\vert}\hline 3 & 0 \\ \hline -1 & 1 \\ \hline \end{tabular} \end{tabular} .$$ (9.63)

Consider computing the security strategy for ${{\rm P}_1}$. Note that $W$ and $Z$ are only one-dimensional subsets of ${\mathbb{R}}^2$. A randomized strategy for ${{\rm P}_1}$ is $w = [w_1 \;\; w_2]$, with $w_1 \geq 0$, $w_2 \geq 0$, and $w_1+w_2 = 1$. Therefore, the domain over which the optimization is performed is $w_1 \in [0,1]$ because $w_2$ can always be derived as $w_2 = 1 - w_1$. Using the first observation above, only the two deterministic strategies for ${{\rm P}_2}$ need to be considered. When considered as linear functions of $w$, these are

$$(3) w_1 + (-1) (1-w_1) = 4 w_1 -1$$ (9.64)

for $z_1 = 1$ and

$$(0) w_1 + (1) (1-w_1) = 1 - w_1$$ (9.65)

for $z_2 = 1$. The lines are plotted in Figure 9.4a. The security strategy is determined by the minimum point along the upper envelope shown in the figure. This is indicated by the thickened line, and it is always a piecewise-linear function in general. The lowest point occurs at $w_1 = 2/5$, and the resulting value is ${\cal L}^*= 3/5$. Therefore, $w^* = [2/5 \;\; 3/5]$.

Figure 9.4: (a) Computing the randomized security strategy, $w^*$, for ${{\rm P}_1}$. (b) Computing the randomized security strategy, $z^*$, for ${{\rm P}_2}$.

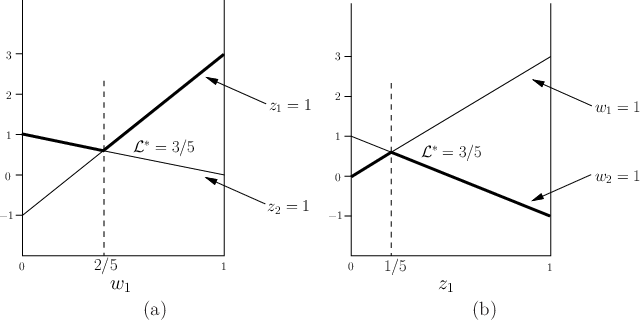A similar procedure can be used to obtain $z^*$. The lines that correspond to the deterministic strategies of ${{\rm P}_1}$ are shown in Figure 9.4b. The security strategy is obtained by finding the maximum value along the lower envelope of the lines, which is shown as the thickened line in the figure. This results in $z^* = [1/5 \;\; 4/5]^T$, and once again, the value is observed as ${\cal L}^*= 3/5$ (this must coincide with the previous one because the randomized upper and lower values are the same!). $\blacksquare$

This procedure appears quite simple if there are only two actions per player. If $n = m = 100$, then the upper and lower envelopes are piecewise-linear functions in ${\mathbb{R}}^{99}$. This may be computationally impractical because all existing linear programming algorithms have running time at least exponential in dimension [264].