Now consider finding the optimal strategy, denoted by 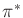 , under
the nondeterministic model. The sets
, under
the nondeterministic model. The sets 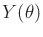 for each
for each
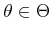 must be used to determine which nature actions are possible
for each observation,
must be used to determine which nature actions are possible
for each observation, 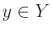 . Let
. Let 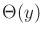 denote this, which
is obtained as
denote this, which
is obtained as
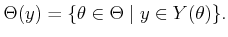 |
(9.23) |
The optimal strategy, 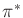 , is defined by setting
, is defined by setting
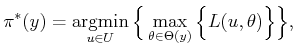 |
(9.24) |
for each 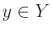 . Compare this to (9.14), in which the
maximum was taken over all
. Compare this to (9.14), in which the
maximum was taken over all 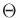 . The advantage of having the
observation,
. The advantage of having the
observation, 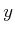 , is that the set is restricted to
, is that the set is restricted to
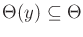 .
.
Under the probabilistic model, an operation analogous to
(9.23) must be performed. This involves computing
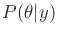 from
from
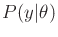 to determine the information that
to determine the information that 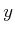 contains regarding
contains regarding 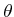 . Using Bayes' rule,
(9.9), with marginalization on the denominator, the
result is
. Using Bayes' rule,
(9.9), with marginalization on the denominator, the
result is
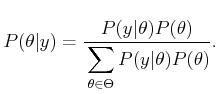 |
(9.25) |
To see the connection between the nondeterministic and probabilistic
cases, define a probability distribution,
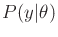 , that is
nonzero only if
, that is
nonzero only if
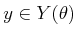 and use a uniform distribution for
and use a uniform distribution for
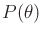 . In this case, (9.25) assigns nonzero
probability to precisely the elements of
. In this case, (9.25) assigns nonzero
probability to precisely the elements of 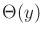 as given in
(9.23). Thus, (9.25) is just the
probabilistic version of (9.23). The optimal strategy,
as given in
(9.23). Thus, (9.25) is just the
probabilistic version of (9.23). The optimal strategy,
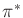 , is specified for each
, is specified for each 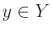 as
as
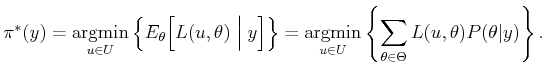 |
(9.26) |
This differs from (9.15) and (9.16) by
replacing 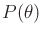 with
with
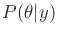 . For each
. For each 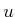 , the
expectation in (9.26) is called the conditional
Bayes' risk. The optimal strategy,
, the
expectation in (9.26) is called the conditional
Bayes' risk. The optimal strategy,
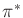 , always selects the strategy that minimizes this risk. Note
that
, always selects the strategy that minimizes this risk. Note
that
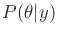 in (9.26) can be expressed using
(9.25), for which the denominator (9.26)
represents
in (9.26) can be expressed using
(9.25), for which the denominator (9.26)
represents 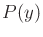 and does not depend on
and does not depend on 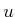 ; therefore, it does not
affect the optimization. Due to this,
; therefore, it does not
affect the optimization. Due to this,
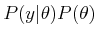 can be
used in the place of
can be
used in the place of
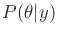 in (9.26), and the
same
in (9.26), and the
same 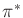 will be obtained. If the spaces are continuous, then
probability densities are used in the place of all probability
distributions, and the method otherwise remains the same.
will be obtained. If the spaces are continuous, then
probability densities are used in the place of all probability
distributions, and the method otherwise remains the same.
Steven M LaValle
2020-08-14

![]() , under
the nondeterministic model. The sets
, under
the nondeterministic model. The sets ![]() for each
for each
![]() must be used to determine which nature actions are possible
for each observation,
must be used to determine which nature actions are possible
for each observation, ![]() . Let
. Let ![]() denote this, which
is obtained as
denote this, which
is obtained as
![]() from
from
![]() to determine the information that
to determine the information that ![]() contains regarding
contains regarding ![]() . Using Bayes' rule,
(9.9), with marginalization on the denominator, the
result is
. Using Bayes' rule,
(9.9), with marginalization on the denominator, the
result is