
Next: 8.5.1.2 Defining a feedback Up: 8.5.1 Computing a Composition Previous: 8.5.1 Computing a Composition
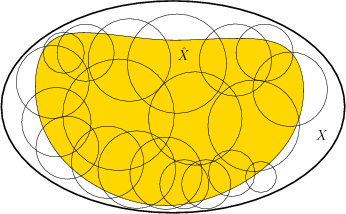 |
Figure 8.15 illustrates the notion of an approximate
cover, which will be used to represent the funnel domains. Let
![]() denote a subset of a state space
denote a subset of a state space ![]() . A cover of
. A cover of
![]() is a collection
is a collection ![]() of sets
for which
of sets
for which
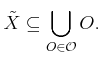 |
(8.50) |
In general, a cover allows the following:
So far, no constraints have been placed on the neighborhoods. They should be chosen in practice to greatly simplify the design of a navigation function over each one. For the original motion planning problem, cell decompositions were designed to make the determination of a collision-free path trivial in each cell. The same idea applies here, except that we now want to construct a feedback plan. Therefore, it is usually assumed that the cells have a simple shape.
A cover is called approximate
if
![]() is a strict subset of
is a strict subset of ![]() . Ideally, we would like to
develop an exact cover, which implies that
. Ideally, we would like to
develop an exact cover, which implies that
![]() and
each neighborhood has some nice property, such as being convex.
Developing such covers is possible in practice for state spaces that
are either low-dimensional or exhibit some special structure. This
was observed for the cell decomposition methods of Chapter
6.
and
each neighborhood has some nice property, such as being convex.
Developing such covers is possible in practice for state spaces that
are either low-dimensional or exhibit some special structure. This
was observed for the cell decomposition methods of Chapter
6.
Consider constructing an approximate cover for ![]() . The goal should
be to cover as much of
. The goal should
be to cover as much of ![]() as possible. This means that
as possible. This means that
![]() should be made as small as possible, in which
should be made as small as possible, in which
![]() denotes Lebesgue measure, as defined in Section
5.1.3. It is also desirable to ensure that
denotes Lebesgue measure, as defined in Section
5.1.3. It is also desirable to ensure that
![]() preserves the connectivity of
preserves the connectivity of ![]() . In other words, if a path between
two points exists in
. In other words, if a path between
two points exists in ![]() , then it should also exist in
, then it should also exist in
![]() .
.
Steven M LaValle 2020-08-14