Euclidean shortest paths

One of the most straightforward notions of optimality is the Euclidean shortest path in ${\mathbb{R}}^2$ or ${\mathbb{R}}^3$. Suppose that ${\cal A}$ is a rigid body that translates only in either ${\cal W}= {\mathbb{R}}^2$ or ${\cal W}= {\mathbb{R}}^3$, which contains an obstacle region ${\cal O}\subset {\cal W}$. Recall that, ordinarily, ${\cal C}_{free}$ is an open set, which means that any path, $\tau: [0,1] \rightarrow {\cal C}_{free}$, can be shortened. Therefore, shortest paths for motion planning must be defined on the closure $\operatorname{cl}({\cal C}_{free})$, which allows the robot to make contact with the obstacles; however, their interiors must not intersect.

For the case in which ${\cal C}_{obs}$ is a polygonal region, the shortest-path roadmap method of Section 6.2.4 has already been given. This can be considered as a kind of multiple-query approach because the roadmap completely captures the structure needed to construct the shortest path for any query. It is possible to make a single-query algorithm using the continuous Dijkstra paradigm [443,708]. This method propagates a wavefront from ${q_{I}}$ and keeps track of critical events in maintaining the wavefront. As events occur, the wavefront becomes composed of wavelets, which are arcs of circles centered on obstacle vertices. The possible events that can occur are 1) a wavelet disappears, 2) a wavelet collides with an obstacle vertex, 3) a wavelet collides with another wavelet, or 4) a wavelet collides with a point in the interior of an obstacle edge. The method can be made to run in time $O(n \lg n)$ and uses $O(n \lg n)$ space. A roadmap is constructed that uses $O(n)$ space. See Section 8.4.3 for a related method.

Figure 7.39: For a polyhedral environment, the shortest paths do not have to cross vertices. Therefore, the shortest-path roadmap method from Section 6.2.4 does not extend to three dimensions.

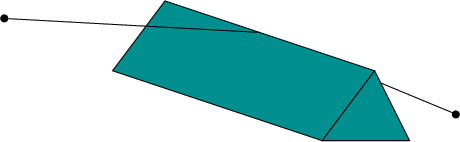Such elegant methods leave the impression that finding shortest paths is not very difficult, but unfortunately they do not generalize nicely to ${\mathbb{R}}^3$ and a polyhedral ${\cal C}_{obs}$. Figure 7.39 shows a simple example in which the shortest path does not have to cross a vertex of ${\cal C}_{obs}$. It may cross anywhere in the interior of an edge; therefore, it is not clear where to draw the bitangent lines that would form the shortest-path roadmap. The lower bounds for this problem are also discouraging. It was shown in [172] that the 3D shortest-path problem in a polyhedral environment is NP-hard. Most of the difficulty arises because of the precision required to represent 3D shortest paths. Therefore, efficient polynomial-time approximation algorithms exist [215,763].