
Next: Spanning tree covering Up: 7.6 Coverage Planning Previous: 7.6 Coverage Planning
One approach to the coverage problem is to decompose
![]() into
cells and perform boustrophedon (from the Greek ``ox turning'')
motions in each cell as shown in Figure 7.35
[222]. It is assumed that the robot is a point in
into
cells and perform boustrophedon (from the Greek ``ox turning'')
motions in each cell as shown in Figure 7.35
[222]. It is assumed that the robot is a point in
![]() , but it carries a tool of thickness
, but it carries a tool of thickness ![]() that hangs
evenly over the sides of the robot. This enables it to paint or mow
part of
that hangs
evenly over the sides of the robot. This enables it to paint or mow
part of
![]() up to distance
up to distance
![]() from either side of the
robot as it moves forward. Such motions are often used in printers to
reduce the number of carriage returns.
from either side of the
robot as it moves forward. Such motions are often used in printers to
reduce the number of carriage returns.
If
![]() is polygonal, a reasonable decomposition can be obtained by
adapting the vertical decomposition method of Section 6.2.2.
In that algorithm, critical events were defined for several cases,
some of which are not relevant for the boustrophedon motions. The
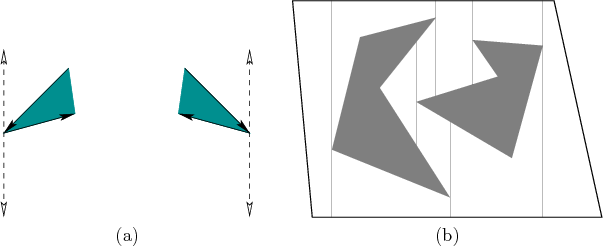
only events that need to be handled are shown in Figure
7.36a [216]. This produces a decomposition
that has fewer cells, as shown in Figure 7.36b.
Even though the cells are nonconvex, they can always be sliced nicely
into vertical strips, which makes them suitable for boustrophedon
motions. The original vertical decomposition could also be used, but
the extra cell boundaries would cause unnecessary repositioning of the
robot. A similar method, which furthermore optimizes the number of
robot turns, is presented in [468].
is polygonal, a reasonable decomposition can be obtained by
adapting the vertical decomposition method of Section 6.2.2.
In that algorithm, critical events were defined for several cases,
some of which are not relevant for the boustrophedon motions. The
only events that need to be handled are shown in Figure
7.36a [216]. This produces a decomposition
that has fewer cells, as shown in Figure 7.36b.
Even though the cells are nonconvex, they can always be sliced nicely
into vertical strips, which makes them suitable for boustrophedon
motions. The original vertical decomposition could also be used, but
the extra cell boundaries would cause unnecessary repositioning of the
robot. A similar method, which furthermore optimizes the number of
robot turns, is presented in [468].
 |
Steven M LaValle 2020-08-14