
Next: Drug design Up: 7.5 Folding Problems in Previous: Carton folding
A knot is a closed curve that does not intersect itself, is
embedded in
![]() , and cannot be untangled to produce a simple loop
(such as a circular path). If the knot is allowed to intersect
itself, then any knot can be untangled; therefore, a careful
definition of what it means to untangle a knot is needed. For a
closed curve,
, and cannot be untangled to produce a simple loop
(such as a circular path). If the knot is allowed to intersect
itself, then any knot can be untangled; therefore, a careful
definition of what it means to untangle a knot is needed. For a
closed curve,
![]() , embedded in
, embedded in
![]() (it
cannot intersect itself), let the set
(it
cannot intersect itself), let the set
![]() of
points not reached by the curve be called the ambient space of
of
points not reached by the curve be called the ambient space of
![]() . In knot theory, an ambient isotopy between two closed
curves,
. In knot theory, an ambient isotopy between two closed
curves, ![]() and
and ![]() , embedded in
, embedded in
![]() is a homeomorphism
between their ambient spaces. Intuitively, this means that
is a homeomorphism
between their ambient spaces. Intuitively, this means that ![]() can be warped into
can be warped into ![]() without allowing any self-intersections.
Therefore, determining whether two loops are equivalent seems closely
related to motion planning. Such equivalence gives rise to groups
that characterize the space of knots and are closely related to the
fundamental group described in Section 4.1.3. For more
information on knot theory, see [8,451,511].
without allowing any self-intersections.
Therefore, determining whether two loops are equivalent seems closely
related to motion planning. Such equivalence gives rise to groups
that characterize the space of knots and are closely related to the
fundamental group described in Section 4.1.3. For more
information on knot theory, see [8,451,511].
A motion planning approach was developed in [571] to
determine whether a closed curve is equivalent to the unknot,
which is completely untangled. This can be expressed as a curve that
maps onto
![]() , embedded in
, embedded in
![]() . The algorithm takes as input a
knot expressed as a circular chain of line segments embedded in
. The algorithm takes as input a
knot expressed as a circular chain of line segments embedded in
![]() . In this case, the unknot can be expressed as a triangle in
. In this case, the unknot can be expressed as a triangle in
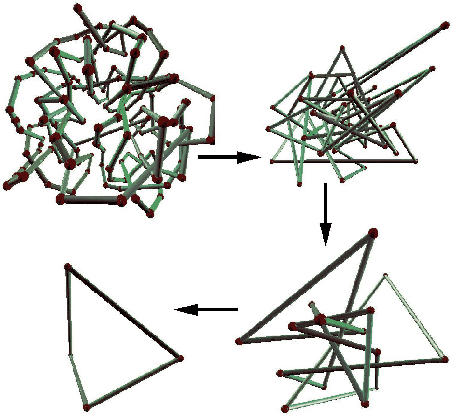
![]() . One of the most challenging examples solved by the planner
is shown in Figure 7.31. The planner is sampling-based
and shares many similarities with the RDT algorithm of Section
5.5 and the Ariadne's clew and expansive space planners
described in Section 5.4.4. Since the task is not to
produce a collision-free path, there are several unique aspects in
comparison to motion planning. An energy function is defined
over the collection of segments to try to guide the search toward
simpler configurations. There are two kinds of local operations that
are made by the planner: 1) Try to move a vertex toward a selected
subgoal in the ambient space. This is obtained by using random
sampling to grow a search tree. 2) Try to delete a vertex, and
connect the neighboring vertices by a straight line. If no collision
occurs along the intermediate configurations, then the knot has been
simplified. The algorithm terminates when it is unable to further
simplify the knot.
. One of the most challenging examples solved by the planner
is shown in Figure 7.31. The planner is sampling-based
and shares many similarities with the RDT algorithm of Section
5.5 and the Ariadne's clew and expansive space planners
described in Section 5.4.4. Since the task is not to
produce a collision-free path, there are several unique aspects in
comparison to motion planning. An energy function is defined
over the collection of segments to try to guide the search toward
simpler configurations. There are two kinds of local operations that
are made by the planner: 1) Try to move a vertex toward a selected
subgoal in the ambient space. This is obtained by using random
sampling to grow a search tree. 2) Try to delete a vertex, and
connect the neighboring vertices by a straight line. If no collision
occurs along the intermediate configurations, then the knot has been
simplified. The algorithm terminates when it is unable to further
simplify the knot.
 |
Steven M LaValle 2020-08-14