Sampling-based methods

Most of the methods of Chapter 5 are not easy to adapt because they require sampling in ${{\cal C}_{fea}}$, for which a parameterization does not exist. If points in a bounded region of ${\mathbb{R}}^n$ are chosen at random, the probability is zero that a point on ${{\cal C}_{fea}}$ will be obtained. Some incremental sampling and searching methods can, however, be adapted by the construction of a local planning method (LPM) that is suited for problems with closure constraints. The sampling-based roadmap methods require many samples to be generated directly on ${{\cal C}_{fea}}$. Section 7.4.2 presents some techniques that can be used to generate such samples for certain classes of problems, enabling the development of efficient sampling-based planners and also improving the efficiency of incremental search planners. Before covering these techniques, we first present a method that leads to a more general sampling-based planner and is easier to implement. However, if designed well, planners based on the techniques of Section 7.4.2 are more efficient.

Figure 7.21: For the RDT, the samples can be drawn from a region in ${\mathbb{R}}^n$, the space in which ${{\cal C}_{clo}}$ is embedded.

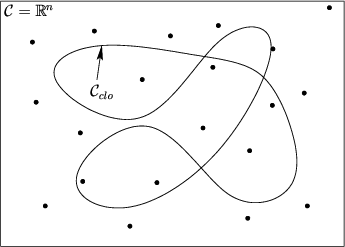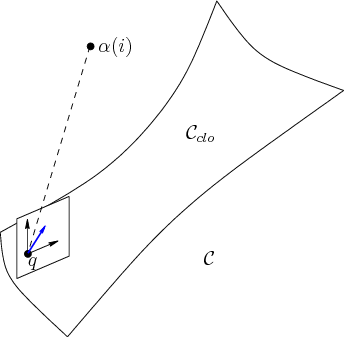
Now consider adapting the RDT of Section 5.5 to work for problems with closure constraints. Similar adaptations may be possible for other incremental sampling and searching methods covered in Section 5.4, such as the randomized potential field planner. A dense sampling sequence, ${\alpha }$, is generated over a bounded $n$-dimensional subset of ${\mathbb{R}}^n$, such as a rectangle or sphere, as shown in Figure 7.21. The samples are not actually required to lie on ${{\cal C}_{clo}}$ because they do not necessarily become part of the topological graph, ${\cal G}$. They mainly serve to pull the search tree in different directions. One concern in choosing the bounding region is that it must include ${{\cal C}_{clo}}$ (at least the connected component that includes ${q_{I}}$) but it must not be unnecessarily large. Such bounds are obtained by analyzing the motion limits for a particular linkage.

Figure 7.22: For each sample ${\alpha }(i)$ the nearest point, $q_n \in {\cal C}$, is found, and then the local planner generates a motion that lies in the local tangent plane. The motion is the project of the vector from $q_n$ to ${\alpha }(i)$ onto the tangent plane.