A state space is defined that considers the configurations of all
robots simultaneously,
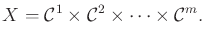 |
(7.6) |
A state 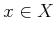 specifies all robot configurations and may be
expressed as
specifies all robot configurations and may be
expressed as
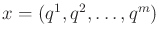 . The dimension of
. The dimension of  is
is
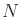 , which is
, which is
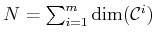 .
.
There are two sources of obstacle regions in the state space: 1) robot-obstacle collisions, and 2) robot-robot collisions. For
each 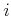 such that
such that
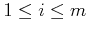 , the subset of
, the subset of  that
corresponds to robot
that
corresponds to robot
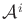 in collision with the obstacle region,
in collision with the obstacle region,
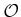 , is
, is
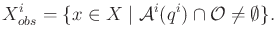 |
(7.7) |
This only models the robot-obstacle collisions.
For each pair,
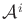 and
and
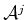 , of robots, the subset of
, of robots, the subset of  that
corresponds to
that
corresponds to
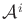 in collision with
in collision with
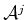 is
is
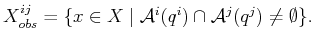 |
(7.8) |
Both (7.7) and (7.8) will be
combined in (7.10) later to yield 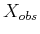 .
.
Formulation 7..2 (Multiple-Robot Motion Planning)
- The world
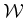 and obstacle region
and obstacle region 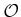 are the
same as in Formulation 4.1.
are the
same as in Formulation 4.1.
- There are
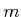 robots,
robots,
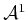 ,
, 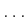 ,
,
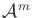 , each of
which may consist of one or more bodies.
, each of
which may consist of one or more bodies.
- Each robot
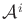 , for
, for 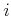 from
from 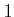 to
to 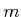 , has an associated
configuration space,
, has an associated
configuration space,
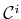 .
.
- The state space
 is defined as the Cartesian product
is defined as the Cartesian product
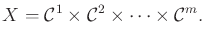 |
(7.9) |
The obstacle region in  is
is
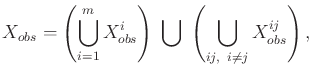 |
(7.10) |
in which 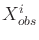 and
and
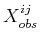 are the robot-obstacle and
robot-robot collision states from (7.7) and
(7.8), respectively.
are the robot-obstacle and
robot-robot collision states from (7.7) and
(7.8), respectively.
- A state
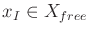 is designated as the initial
state, in which
is designated as the initial
state, in which
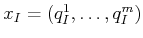 . For each
. For each 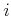 such that
such that
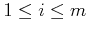 ,
, 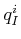 specifies the initial
configuration of
specifies the initial
configuration of
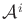 .
.
- A state
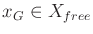 is designated as the goal
state, in which
is designated as the goal
state, in which
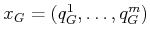 .
.
- The task is to compute a continuous path
![$ \tau: [0,1] \rightarrow
X_{free}$](img2622.gif) such that
such that
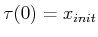 and
and
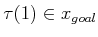 .
.
Subsections
Steven M LaValle
2020-08-14

![]() such that
such that
![]() , the subset of
, the subset of ![]() that
corresponds to robot
that
corresponds to robot
![]() in collision with the obstacle region,
in collision with the obstacle region,
![]() , is
, is
![]() and
and
![]() , of robots, the subset of
, of robots, the subset of ![]() that
corresponds to
that
corresponds to
![]() in collision with
in collision with
![]() is
is