Many sampling-based methods can be adapted from  to
to  without
much difficulty. The time dependency of obstacle models must be taken
into account when verifying that path segments are collision-free; the
techniques from Section 5.3.4 can be extended to handle
this. One important concern is the metric for
without
much difficulty. The time dependency of obstacle models must be taken
into account when verifying that path segments are collision-free; the
techniques from Section 5.3.4 can be extended to handle
this. One important concern is the metric for  . For some
algorithms, it may be important to permit the use of a
pseudometric because symmetry is broken by time (going backward
in time is not as easy as going forward).
. For some
algorithms, it may be important to permit the use of a
pseudometric because symmetry is broken by time (going backward
in time is not as easy as going forward).
For example, suppose that the C-space  is a metric
space,
is a metric
space,
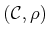 . The metric can be extended across time to obtain
a pseudometric,
. The metric can be extended across time to obtain
a pseudometric, 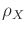 , as follows. For a pair of states,
, as follows. For a pair of states, 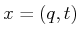 and
and
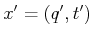 , let
, let
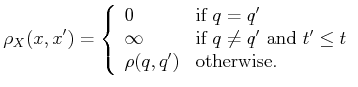 |
(7.3) |
Using 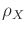 , several sampling-based methods naturally work. For
example, RDTs from Section
5.5 can be adapted to
, several sampling-based methods naturally work. For
example, RDTs from Section
5.5 can be adapted to  . Using
. Using 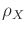 for a single-tree
approach ensures that all path segments travel forward in time. Using
bidirectional approaches is more difficult for time-varying problems
because
for a single-tree
approach ensures that all path segments travel forward in time. Using
bidirectional approaches is more difficult for time-varying problems
because 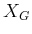 is usually not a single point. It is not clear which
is usually not a single point. It is not clear which
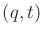 should be the starting vertex for the tree from the goal; one
possibility is to initialize the goal tree to an entire time-invariant
segment. The sampling-based roadmap methods of Section
5.6 are perhaps the most straightforward to adapt.
The notion of a directed roadmap is
needed, in which every edge must be directed to yield a
time-monotonic path. For each pair of states,
should be the starting vertex for the tree from the goal; one
possibility is to initialize the goal tree to an entire time-invariant
segment. The sampling-based roadmap methods of Section
5.6 are perhaps the most straightforward to adapt.
The notion of a directed roadmap is
needed, in which every edge must be directed to yield a
time-monotonic path. For each pair of states, 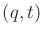 and
and
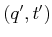 , such that
, such that
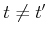 , exactly one
valid direction exists for making a potential edge. If
, exactly one
valid direction exists for making a potential edge. If
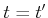 , then no edge can be attempted because it would require the
robot to instantaneously ``teleport'' from one part of
, then no edge can be attempted because it would require the
robot to instantaneously ``teleport'' from one part of 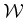 to
another. Since forward time progress is already taken into account by
the directed edges, a symmetric metric may be preferable instead of
(7.3) for the sampling-based roadmap approach.
to
another. Since forward time progress is already taken into account by
the directed edges, a symmetric metric may be preferable instead of
(7.3) for the sampling-based roadmap approach.
Steven M LaValle
2020-08-14

![]() to
to ![]() without
much difficulty. The time dependency of obstacle models must be taken
into account when verifying that path segments are collision-free; the
techniques from Section 5.3.4 can be extended to handle
this. One important concern is the metric for
without
much difficulty. The time dependency of obstacle models must be taken
into account when verifying that path segments are collision-free; the
techniques from Section 5.3.4 can be extended to handle
this. One important concern is the metric for ![]() . For some
algorithms, it may be important to permit the use of a
pseudometric because symmetry is broken by time (going backward
in time is not as easy as going forward).
. For some
algorithms, it may be important to permit the use of a
pseudometric because symmetry is broken by time (going backward
in time is not as easy as going forward).
![]() is a metric
space,
is a metric
space,
![]() . The metric can be extended across time to obtain
a pseudometric,
. The metric can be extended across time to obtain
a pseudometric, ![]() , as follows. For a pair of states,
, as follows. For a pair of states, ![]() and
and
![]() , let
, let