6.2.3 Maximum-Clearance Roadmaps

Figure 6.8: The maximum clearance roadmap keeps as far away from the ${\cal C}_{obs}$ as possible. This involves traveling along points that are equidistant from two or more points on the boundary of ${\cal C}_{obs}$.

Figure 6.9: Voronoi roadmap pieces are generated in one of three possible cases. The third case leads to a quadratic curve.

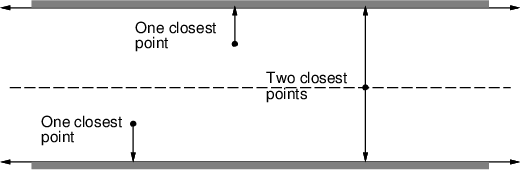
A maximum-clearance roadmap tries to keep as far as possible from ${\cal C}_{obs}$, as shown for the corridor in Figure 6.8. The resulting solution paths are sometimes preferred in mobile robotics applications because it is difficult to measure and control the precise position of a mobile robot. Traveling along the maximum-clearance roadmap reduces the chances of collisions due to these uncertainties. Other names for this roadmap are generalized Voronoi diagram and retraction method [749]. It is considered as a generalization of the Voronoi diagram (recall from Section 5.2.2) from the case of points to the case of polygons. Each point along a roadmap edge is equidistant from two points on the boundary of ${\cal C}_{obs}$. Each roadmap vertex corresponds to the intersection of two or more roadmap edges and is therefore equidistant from three or more points along the boundary of ${\cal C}_{obs}$.

The retraction term comes from topology and provides a nice intuition about the method. A subspace $S$ is a deformation retract of a topological space $X$ if the following continuous homotopy, $h : X \times [0,1] \rightarrow X$, can be defined as follows [451]:

1. $h(x,0) = x$ for all $x \in X$.
2. $h(x,1)$ is a continuous function that maps every element of $X$ to some element of $S$.
3. For all $t \in [0,1]$, $h(s,t) = s$ for any $s \in S$.

The intuition is that ${\cal C}_{free}$ is gradually thinned through the homotopy process, until a skeleton, $S$, is obtained. An approximation to this shrinking process can be imagined by shaving off a thin layer around the whole boundary of ${\cal C}_{free}$. If this is repeated iteratively, the maximum-clearance roadmap is the only part that remains (assuming that the shaving always stops when thin ``slivers'' are obtained).

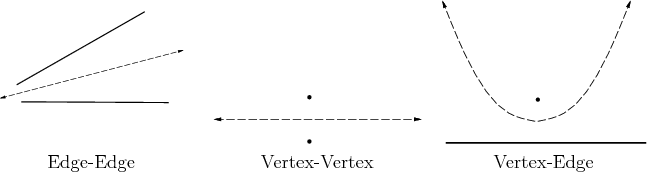
To construct the maximum-clearance roadmap, the concept of features from Section 5.3.3 is used again. Let the feature set refer to the set of all edges and vertices of ${\cal C}_{obs}$. Candidate paths for the roadmap are produced by every pair of features. This leads to a naive $O(n^4)$ time algorithm as follows. For every edge-edge feature pair, generate a line as shown in Figure 6.9a. For every vertex-vertex pair, generate a line as shown in Figure 6.9b. The maximum-clearance path between a point and a line is a parabola. Thus, for every edge-point pair, generate a parabolic curve as shown in Figure 6.9c. The portions of the paths that actually lie on the maximum-clearance roadmap are determined by intersecting the curves. Several algorithms exist that provide better asymptotic running times [616,626], but they are considerably more difficult to implement. The best-known algorithm runs in $O(n \lg n)$ time in which $n$ is the number of roadmap curves [865].