
Next: 5.6.2 Visibility Roadmap Up: 5.6.1 The Basic Method Previous: Query phase
There have been many works that analyze the performance of
sampling-based roadmaps. The basic idea from one of them
[69] is briefly presented here. Consider
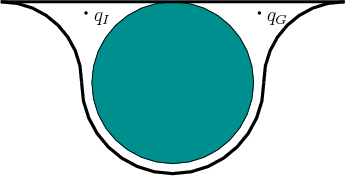
problems such as the one in Figure 5.27, in which the CONNECT method will mostly likely fail in the thin tube, even though
a connection exists. The higher dimensional versions of these
problems are even more difficult. Many planning problems involve
moving a robot through an area with tight clearance. This generally
causes narrow channels to form in
![]() , which leads to a
challenging planning problem for the sampling-based roadmap algorithm.
Finding the escape of a bug trap is also challenging, but for the
roadmap methods, even traveling through a single corridor is hard
(unless more sophisticated LPMs are used
[479]).
, which leads to a
challenging planning problem for the sampling-based roadmap algorithm.
Finding the escape of a bug trap is also challenging, but for the
roadmap methods, even traveling through a single corridor is hard
(unless more sophisticated LPMs are used
[479]).
 |
Let ![]() denote the set of all configurations that can be connected
to
denote the set of all configurations that can be connected
to ![]() using the CONNECT method. Intuitively, this is
considered as the set of all configurations that can be ``seen'' using
line-of-sight visibility, as shown in Figure 5.28a
using the CONNECT method. Intuitively, this is
considered as the set of all configurations that can be ``seen'' using
line-of-sight visibility, as shown in Figure 5.28a
The ![]() -goodness of
-goodness of
![]() is defined as
is defined as
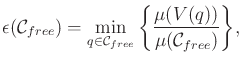 |
(5.41) |
Steven M LaValle 2020-08-14