Making good grids

Figure 5.5: The Sukharev grid and a nongrid lattice.

Optimizing dispersion forces the points to be distributed more uniformly over ${\cal C}$. This causes them to fail statistical tests, but the point distribution is often better for motion planning purposes. Consider the best way to reduce dispersion if $\rho$ is the $L_\infty$ metric and $X = [0,1]^n$. Suppose that the number of samples, $k$, is given. Optimal dispersion is obtained by partitioning $[0,1]$ into a grid of cubes and placing a point at the center of each cube, as shown for $n=2$ and $k=196$ in Figure 5.5a. The number of cubes per axis must be $\lfloor k^\frac{1}{n} \rfloor$, in which $\lfloor\cdot\rfloor$ denotes the floor. If $k^\frac{1}{n}$ is not an integer, then there are leftover points that may be placed anywhere without affecting the dispersion. Notice that $k^\frac{1}{n}$ just gives the number of points per axis for a grid of $k$ points in $n$ dimensions. The resulting grid will be referred to as a Sukharev grid [922].

The dispersion obtained by the Sukharev grid is the best possible. Therefore, a useful lower bound can be given for any set $P$ of $k$ samples [922]:

$$\delta(P) \geq { 1 \over 2 \big\lfloor k^\frac{1}{d} \big\rfloor}.$$ (5.20)

This implies that keeping the dispersion fixed requires exponentially many points in the dimension, $d$.

At this point you might wonder why $L_\infty$ was used instead of $L_2$, which seems more natural. This is because the $L_2$ case is extremely difficult to optimize (except in ${\mathbb{R}}^2$, where a tiling of equilateral triangles can be made, with a point in the center of each one). Even the simple problem of determining the best way to distribute a fixed number of points in $[0,1]^3$ is unsolved for most values of $k$. See [241] for extensive treatment of this problem.

Suppose now that other topologies are considered instead of $[0,1]^n$. Let $X = [0,1]{/\sim}$, in which the identification produces a torus. The situation is quite different because $X$ no longer has a boundary. The Sukharev grid still produces optimal dispersion, but it can also be shifted without increasing the dispersion. In this case, a standard grid may also be used, which has the same number of points as the Sukharev grid but is translated to the origin. Thus, the first grid point is $(0,0)$, which is actually the same as $2^n-1$ other points by identification. If $X$ represents a cylinder and the number of points, $k$, is given, then it is best to just use the Sukharev grid. It is possible, however, to shift each coordinate that behaves like ${\mathbb{S}}^1$. If $X$ is rectangular but not a square, a good grid can still be made by tiling the space with cubes. In some cases this will produce optimal dispersion. For complicated spaces such as $SO(3)$, no grid exists in the sense defined so far. It is possible, however, to generate grids on the faces of an inscribed Platonic solid [251] and lift the samples to ${\mathbb{S}}^n$ with relatively little distortion [987]. For example, to sample ${\mathbb{S}}^2$, Sukharev grids can be placed on each face of a cube. These are lifted to obtain the warped grid shown in Figure 5.6a.

Figure 5.6: (a) A distorted grid can even be placed over spheres and $SO(3)$ by putting grids on the faces of an inscribed cube and lifting them to the surface [987]. (b) A lattice can be considered as a grid in which the generators are not necessarily orthogonal.

Example 5..15 (Sukharev Grid)   Suppose that $n=2$ and $k = 9$. If $X = [0,1]^2$, then the Sukharev grid yields points for the nine cases in which either coordinate may be $1/6$, $1/2$, or $5/6$. The $L_\infty$ dispersion is $1/6$. The spacing between the points along each axis is $1/3$, which is twice the dispersion. If instead $X = [0,1]^2{/\sim}$, which represents a torus, then the nine points may be shifted to yield the standard grid. In this case each coordinate may be 0, $1/3$, or $2/3$. The dispersion and spacing between the points remain unchanged. $\blacksquare$

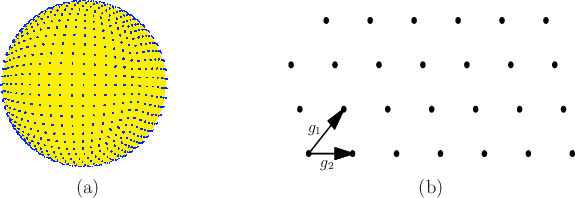One nice property of grids is that they have a lattice structure. This means that neighboring points can be obtained very easily be adding or subtracting vectors. Let $g_j$ be an $n$-dimensional vector called a generator. A point on a lattice can be expressed as

$$x = \sum_{j=1}^n k_j g_j$$ (5.21)

for $n$ independent generators, as depicted in Figure 5.6b. In a 2D grid, the generators represent ``up'' and ``right.'' If $X = [0,100]^2$ and a standard grid with integer spacing is used, then the neighbors of the point $(50,50)$ are obtained by adding $(0,1)$, $(0,-1)$, $(-1,0)$, or $(1,0)$. In a general lattice, the generators need not be orthogonal. An example is shown in Figure 5.5b. In Section 5.4.2, lattice structure will become important and convenient for defining the search graph.