One has to be very careful about sampling uniformly over the space of
rotations. The probability density must correspond to the Haar
measure, which means that a random rotation should be obtained by
picking a point at random on
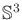 and forming the unit quaternion.
An extremely clever way to sample
and forming the unit quaternion.
An extremely clever way to sample 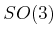 uniformly at random is given
in [883] and is reproduced here. Choose three points
uniformly at random is given
in [883] and is reproduced here. Choose three points
![$ u_1,u_2,u_3 \in [0,1]$](img1809.gif) uniformly at random. A uniform, random
quaternion is given by the simple expression
uniformly at random. A uniform, random
quaternion is given by the simple expression
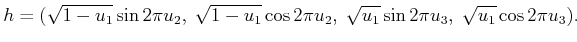 |
(5.15) |
A full explanation of the method is given in [883], and a brief
intuition is given here. First drop down a dimension and pick
![$ u_1,u_2 \in [0,1]$](img1811.gif) to generate points on
to generate points on
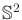 . Let
. Let 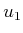 represent
the value for the third coordinate,
represent
the value for the third coordinate,
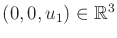 . The slice
of points on
. The slice
of points on
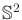 for which
for which 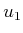 is fixed for
is fixed for
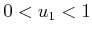 yields
a circle on
yields
a circle on
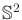 that corresponds to some line of latitude on
that corresponds to some line of latitude on
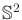 . The second parameter selects the longitude,
. The second parameter selects the longitude, 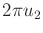 .
Fortunately, the points are uniformly distributed over
.
Fortunately, the points are uniformly distributed over
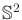 . Why?
Imagine
. Why?
Imagine
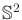 as the crust on a spherical loaf of bread that is run
through a bread slicer. The slices are cut in a direction parallel to
the equator and are of equal thickness. The crusts of each slice have
equal area; therefore, the points are uniformly distributed. The
method proceeds by using that fact that
as the crust on a spherical loaf of bread that is run
through a bread slicer. The slices are cut in a direction parallel to
the equator and are of equal thickness. The crusts of each slice have
equal area; therefore, the points are uniformly distributed. The
method proceeds by using that fact that
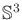 can be partitioned into
a spherical arrangement of circles (known as the Hopf fibration);
there is an
can be partitioned into
a spherical arrangement of circles (known as the Hopf fibration);
there is an
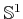 copy for each point in
copy for each point in
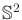 . The method above is
used to provide a random point on
. The method above is
used to provide a random point on
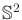 using
using 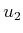 and
and 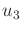 , and
, and
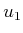 produces a random point on
produces a random point on
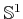 ; they are carefully combined
in (5.15) to yield a random rotation. To respect the
antipodal identification for rotations, any quaternion
; they are carefully combined
in (5.15) to yield a random rotation. To respect the
antipodal identification for rotations, any quaternion 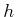 found in
the lower hemisphere (i.e.,
found in
the lower hemisphere (i.e., 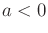 ) can be negated to yield
) can be negated to yield 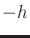 .
This does not distort the uniform random distribution of the samples.
.
This does not distort the uniform random distribution of the samples.
Steven M LaValle
2020-08-14
