
Next: Varieties Up: 4.4.1 Mathematical Concepts Previous: Fields
Suppose there are ![]() variables,
variables,
![]() . A
monomial over a field
. A
monomial over a field
![]() is a product of the form
is a product of the form
A polynomial ![]() in variables
in variables
![]() with
coefficients in
with
coefficients in
![]() is a finite linear combination of monomials that
have coefficients in
is a finite linear combination of monomials that
have coefficients in
![]() . A polynomial can be expressed as
. A polynomial can be expressed as
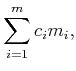 |
(4.48) |
| (4.50) |
The set
![]() of polynomials is actually a group
with respect to addition; however, it is not a field. Even though
polynomials can be multiplied, some polynomials do not have a
multiplicative inverse. Therefore, the set
of polynomials is actually a group
with respect to addition; however, it is not a field. Even though
polynomials can be multiplied, some polynomials do not have a
multiplicative inverse. Therefore, the set
![]() is
often referred to as a commutative ring of polynomials. A
commutative ring is a set with two operations for which every axiom
for fields is satisfied except the last one, which would require a
multiplicative inverse.
is
often referred to as a commutative ring of polynomials. A
commutative ring is a set with two operations for which every axiom
for fields is satisfied except the last one, which would require a
multiplicative inverse.
Steven M LaValle 2020-08-14