2D manifolds

Many important, 2D manifolds can be defined by applying the Cartesian product to 1D manifolds. The 2D manifold ${\mathbb{R}}^2$ is formed by ${\mathbb{R}}\times {\mathbb{R}}$. The product ${\mathbb{R}}\times {\mathbb{S}}^1$ defines a manifold that is equivalent to an infinite cylinder. The product ${\mathbb{S}}^1 \times {\mathbb{S}}^1$ is a manifold that is equivalent to a torus (the surface of a donut).

Figure 4.5: Some 2D manifolds that can be obtained by identifying pairs of points along the boundary of a square region.

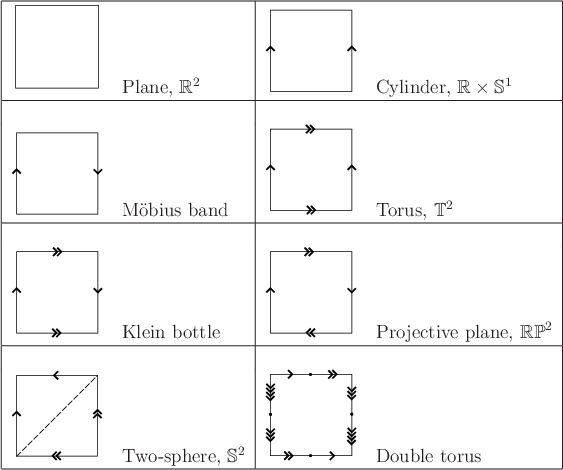Can any other 2D manifolds be defined? See Figure 4.5. The identification idea can be applied to generate several new manifolds. Start with an open square $M = (0,1) \times (0,1)$, which is homeomorphic to ${\mathbb{R}}^2$. Let $(x,y)$ denote a point in the plane. A flat cylinder is obtained by making the identification $(0,y) \sim (1,y)$ for all $y \in (0,1)$ and adding all of these points to $M$. The result is depicted in Figure 4.5 by drawing arrows where the identification occurs.

A Möbius band can be constructed by taking a strip of paper and connecting the ends after making a 180-degree twist. This result is not homeomorphic to the cylinder. The Möbius band can also be constructed by putting the twist into the identification, as $(0,y) \sim (1,1-y)$ for all $y \in (0,1)$. In this case, the arrows are drawn in opposite directions. The Möbius band has the famous properties that it has only one side (trace along the paper strip with a pencil, and you will visit both sides of the paper) and is nonorientable (if you try to draw it in the plane, without using identification tricks, it will always have a twist).

For all of the cases so far, there has been a boundary to the set. The next few manifolds will not even have a boundary, even though they may be bounded. If you were to live in one of them, it means that you could walk forever along any trajectory and never encounter the edge of your universe. It might seem like our physical universe is unbounded, but it would only be an illusion. Furthermore, there are several distinct possibilities for the universe that are not homeomorphic to each other. In higher dimensions, such possibilities are the subject of cosmology, which is a branch of astrophysics that uses topology to characterize the structure of our universe.

A torus can be constructed by performing identifications of the form $(0,y) \sim (1,y)$, which was done for the cylinder, and also $(x,0) \sim (x,1)$, which identifies the top and bottom. Note that the point $(0,0)$ must be included and is identified with three other points. Double arrows are used in Figure 4.5 to indicate the top and bottom identification. All of the identification points must be added to $M$. Note that there are no twists. A funny interpretation of the resulting flat torus is as the universe appears for a spacecraft in some 1980s-style Asteroids-like video games. The spaceship flies off of the screen in one direction and appears somewhere else, as prescribed by the identification.

Two interesting manifolds can be made by adding twists. Consider performing all of the identifications that were made for the torus, except put a twist in the side identification, as was done for the Möbius band. This yields a fascinating manifold called the Klein bottle, which can be embedded in ${\mathbb{R}}^4$ as a closed 2D surface in which the inside and the outside are the same! (This is in a sense similar to that of the Möbius band.) Now suppose there are twists in both the sides and the top and bottom. This results in the most bizarre manifold yet: the real projective plane, ${\mathbb{RP}}^2$. This space is equivalent to the set of all lines in ${\mathbb{R}}^3$ that pass through the origin. The 3D version, ${\mathbb{RP}}^3$, happens to be one of the most important manifolds for motion planning!

Let ${\mathbb{S}}^2$ denote the unit sphere, which is defined as

$${\mathbb{S}}^2 = \{ (x,y,z) \in {\mathbb{R}}^3 \;\vert\; x^2 + y^2 + z^2 = 1 \} .$$ (4.6)

Another way to represent ${\mathbb{S}}^2$ is by making the identifications shown in the last row of Figure 4.5. A dashed line is indicated where the equator might appear, if we wanted to make a distorted wall map of the earth. The poles would be at the upper left and lower right corners. The final example shown in Figure 4.5 is a double torus, which is the surface of a two-holed donut.