The set
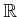 of reals is the most obvious example of a 1D manifold
because
of reals is the most obvious example of a 1D manifold
because
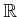 certainly looks like (via homeomorphism)
certainly looks like (via homeomorphism)
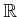 in the
vicinity of every point. The range can be restricted to the unit
interval to yield the manifold
in the
vicinity of every point. The range can be restricted to the unit
interval to yield the manifold 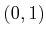 because they are homeomorphic
(recall Example 4.5).
because they are homeomorphic
(recall Example 4.5).
Another 1D manifold, which is not homeomorphic to 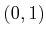 , is a
circle,
, is a
circle,
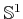 . In this case
. In this case
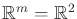 , and let
, and let
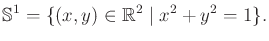 |
(4.5) |
If you are thinking like a topologist, it should appear that this
particular circle is not important because there are numerous ways to
define manifolds that are homeomorphic to
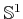 . For any manifold
that is homeomorphic to
. For any manifold
that is homeomorphic to
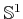 , we will sometimes say that the
manifold is
, we will sometimes say that the
manifold is
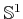 , just represented in a different way. Also,
, just represented in a different way. Also,
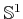 will be called a circle, but this is meant only in the
topological sense; it only needs to be homeomorphic to the circle that
we learned about in high school geometry. Also, when referring to
will be called a circle, but this is meant only in the
topological sense; it only needs to be homeomorphic to the circle that
we learned about in high school geometry. Also, when referring to
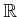 , we might instead substitute
, we might instead substitute 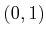 without any trouble. The
alternative representations of a manifold can be considered as
changing parameterizations, which are
formally introduced in Section 8.3.2.
without any trouble. The
alternative representations of a manifold can be considered as
changing parameterizations, which are
formally introduced in Section 8.3.2.
Steven M LaValle
2020-08-14

![]() of reals is the most obvious example of a 1D manifold
because
of reals is the most obvious example of a 1D manifold
because
![]() certainly looks like (via homeomorphism)
certainly looks like (via homeomorphism)
![]() in the
vicinity of every point. The range can be restricted to the unit
interval to yield the manifold
in the
vicinity of every point. The range can be restricted to the unit
interval to yield the manifold ![]() because they are homeomorphic
(recall Example 4.5).
because they are homeomorphic
(recall Example 4.5).
![]() , is a
circle,
, is a
circle,
![]() . In this case
. In this case
![]() , and let
, and let